Question

Please help answer questions one through fiveApply the transformation (a to c) on ABC to get an image

Answer 1

d) area of the pre- image will be less than the new image

e) it is

Step-by-step explanation:

Given:

Triangle ABC on a coordinate plane

To find:

the transformation on the original image

We need to state the vertices of the triangle ABC:

A = (-1, 2)

B = (-2, 1)

C = (0, 0)

a) dilation by a scale factor of 4

b) reflect over the x axis:

`\begin{gathered} (x,\text{ y\rparen }\rightarrow\text{ \lparen x, -y\rparen} \\ We\text{ will negate all the y values of the vertices above while keeping x coordinate constant} \\ A\text{ = \lparen-4, -8\rparen} \\ B\text{ = \lparen-8, -4\rparen} \\ C=\text{ \lparen0, -0\rparen = \lparen0, 0\rparen} \end{gathered}`

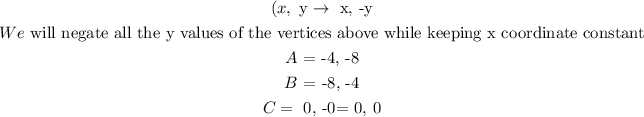
c) dilate by 1/2

`\begin{gathered} (x,\text{ y\rparen }\rightarrow((1)/(2)x,\text{ }(1)/(2)y) \\ We\text{ will multiply the coordinates above by 1/2 in both the x and y coordinates} \\ A^(\prime)\text{ = \lparen}(1)/(2)(-4),\text{ }(1)/(2)(-8))\text{ = \lparen-2, -4\rparen} \\ B^(\prime)\text{ = \lparen}(1)/(2)(-8),\text{ }(1)/(2)(-4))\text{ = \lparen-4, -2\rparen} \\ C^(\prime)\text{ = \lparen}(1)/(2)(0),\text{ }(1)/(2)(0))\text{ = \lparen0, 0\rparen} \\ \\ Image\text{ of ABC: A' \lparen-2, -4\rparen, B' \lparen-4, -2\rparen and C' = \lparen0, 0\rparen} \end{gathered}`

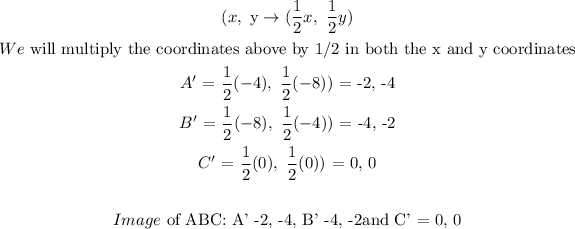
d) To determine if the area of the pre-image is greater or less than, we will plot the coordinates of both triangles:

Since the triangle of the Image is greater than the triangle of the pre-image (original figure), then the area of the pre- image will be less than the new image

e) For two triangles to be congruent, the sides and angles for both triangles will be equal

For two triangles to be similar, the ratio of their corresponding sides will be equal

The image A'B'C' is a scaled triangle of ABC. This mean the sides can't be equal but the ratio fo their corresponding sides will be equal.

Hence, it is simlar