Question

Write an equation for the line that contains (-32, -12) and is perpendicularto the graph -8x + 10y = 40Can anyone that KNOWS the answer help?

Answer 1

The first step is finding the slope of the equation -8x + 10y = 40.

To do so, let's put this equation in the slope-intercept form: y = mx + b, where m is the slope.

So we have:

`\begin{gathered} -8x+10y=40 \\ -4x+5y=20 \\ 5y=4x+20 \\ y=(4)/(5)x+4 \end{gathered}`

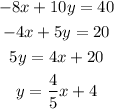
Then, since the line we want is perpendicular to this given line, their slopes have the following relation:

`m_2=-(1)/(m_1)`

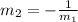
So, calculating the slope of the line, we have:

`m_2=-(1)/((4)/(5))=-(5)/(4)`

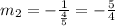
Finally, our equation has the point (-32, -12) as a solution, so we have:

`\begin{gathered} y=mx+b \\ y=-(5)/(4)x+b \\ -12=-(5)/(4)\cdot(-32)+b \\ -12=-5\cdot(-8)+b \\ -12=40+b \\ b=-12-40 \\ b=-52 \end{gathered}`

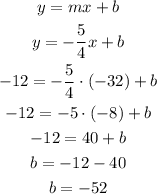
So our equation is y = (-5/4)x - 52