Question

A wheel of radius 30.0 cm is rotating at a rate of 2.30 revolutions every 0.0810 s. The linear speed of a point on the wheel’s rim = 178 radWhat is the linear speed of a point on the wheel’s rim?What is the wheel’s frequency of rotation?

Answer 1

Given data

*The given radius of the wheel is r = 30.0 cm = 0.30 m

*The given angle of the wheel rotates in 1.00 s is

`\theta=178.0\text{ rad}`

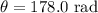
*The angular velocity of the wheel is

`\omega=178.0\text{ rad/s}`

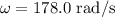
The formula for the linear speed of a point on the wheel's rim is given as

`v=r\omega`

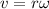
Substitute the known values in the above expression as

`\begin{gathered} v=(0.30)(178.0) \\ =53.4\text{ m/s} \end{gathered}`

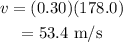
Hence, the linear speed of a point on the wheel's rim is v = 53.4 m/s

The formula for the wheel's frequency of rotation is given as

`\begin{gathered} \omega=2\pi f \\ f=(\omega)/(2\pi) \end{gathered}`

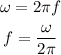
Substitute the known values in the above expression as

`\begin{gathered} f=(178.0)/(2*3.14) \\ =28.34\text{ Hz} \end{gathered}`

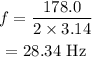
Hence, the wheel's frequency of rotation is f = 28.34 Hz