Given data
*The given radius of the wheel is r = 30.0 cm = 0.30 m
*The given angle of the wheel rotates in 1.00 s is
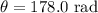
*The angular velocity of the wheel is

The formula for the linear speed of a point on the wheel's rim is given as
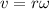
Substitute the known values in the above expression as

Hence, the linear speed of a point on the wheel's rim is v = 53.4 m/s
The formula for the wheel's frequency of rotation is given as

Substitute the known values in the above expression as

Hence, the wheel's frequency of rotation is f = 28.34 Hz