Question

What is the solution to the system of equationsy = 3x - 2 and y = g(x) where g(x) is defined bythe function below?y=g(x)

Answer 1

we need to write the equation of the graph

it is a parable then the general form is

`y=(x+a)^2+b`

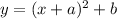
where a move the parable horizontally from the origin (a=negative move to right and a=positive move to left)

and b move the parable vertically from the origin (b=negative move to down and b=positive move to up)

this parable was moving from the origin to the right 2 units and any vertically

then a is -2 and b 0

`y=(x-2)^2`

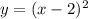
now we have the system of equations

`\begin{gathered} y=3x-2 \\ y=(x-2)^2 \end{gathered}`

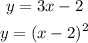
we can replace the y of the first equation on the second and give us

`3x-2=(x-2)^2`

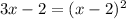
simplify

`3x-2=x^2-4x+4`

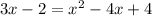
we need to solve x but we have terms sith x and x^2 then we can equal to 0 to factor

`\begin{gathered} 3x-2-x^2+4x-4=0 \\ -x^2+7x-6=0 \end{gathered}`

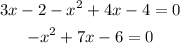
multiply on both sides to remove the negative sign on x^2

`x^2-7x+6=0`

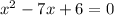
now we use the quadratic formula

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

where a is 1, b is -7 and c is 6

`\begin{gathered} x=\frac{-(-7)\pm\sqrt[]{(-7)^2-4(1)(6)}}{2(1)} \\ \\ x=\frac{7\pm\sqrt[]{49-24}}{2} \\ \\ x=\frac{7\pm\sqrt[]{25}}{2} \\ \\ x=(7\pm5)/(2) \end{gathered}`

we have two solutions for x

`\begin{gathered} x_1=(7+5)/(2)=6 \\ \\ x_2=(7-5)/(2)=1 \end{gathered}`

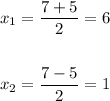
now we replace the values of x on the first equation to find the corresponding values of y

`y=3x-2`

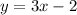
x=6

`\begin{gathered} y=3(6)-2 \\ y=16 \end{gathered}`

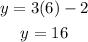
x=1

`\begin{gathered} y=3(1)-2 \\ y=1 \end{gathered}`

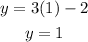
Then we have to pairs of solutions

`\begin{gathered} (6,16) \\ (1,1) \end{gathered}`

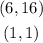
where green line is y=3x-2

and red points are the solutions (1,1)and(6,16)