we need to write the equation of the graph
it is a parable then the general form is
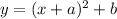
where a move the parable horizontally from the origin (a=negative move to right and a=positive move to left)
and b move the parable vertically from the origin (b=negative move to down and b=positive move to up)
this parable was moving from the origin to the right 2 units and any vertically
then a is -2 and b 0

now we have the system of equations
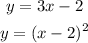
we can replace the y of the first equation on the second and give us
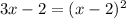
simplify
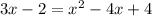
we need to solve x but we have terms sith x and x^2 then we can equal to 0 to factor
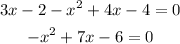
multiply on both sides to remove the negative sign on x^2
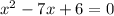
now we use the quadratic formula
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
where a is 1, b is -7 and c is 6
![\begin{gathered} x=\frac{-(-7)\pm\sqrt[]{(-7)^2-4(1)(6)}}{2(1)} \\ \\ x=\frac{7\pm\sqrt[]{49-24}}{2} \\ \\ x=\frac{7\pm\sqrt[]{25}}{2} \\ \\ x=(7\pm5)/(2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1c4w67ts66w8dnb73wph85wdrn2sromdrv.png)
we have two solutions for x
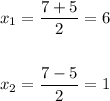
now we replace the values of x on the first equation to find the corresponding values of y
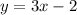
x=6
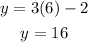
x=1
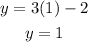
Then we have to pairs of solutions
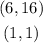
where green line is y=3x-2
and red points are the solutions (1,1)and(6,16)