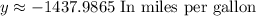Given the values shown in the table, let be "x" the Vehicle weight (in hundreds of lbs.) and "y" the City MPG (Miles per gallon).
1. Given the points:
![(27,25),(35,19),(39,16),(32,21),(40,15),(23,29),(18,31),(37,15),(17,46),(23,26),(37,17),(30,26),(23,29),(32,19),(20,33),(30,21)]()
You can plot them on a Coordinate Plane:
2. Notice the following line:
Notice that the points are closed to the red line that has a negative slope. Therefore, you can identify that when one of the variables increases, the other variable decreases. Hence, you can conclude that the data describes a negative correlation.
3. You need to follow these steps to find the equation of the line of best fit:
- You need to find the average of the x-values by adding them and dividing the Sum by the number of x-values:
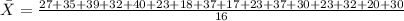
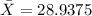
- Find the average of the y-values:
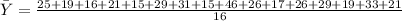
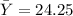
- Find:
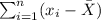
Where this represents each x-values in the data set:
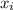
You get:

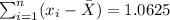
- Find:
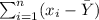
You get:
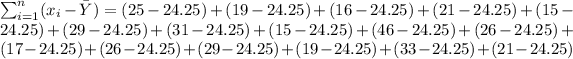
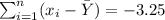
- Find:
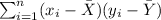
You get:
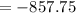
- Find:
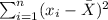
You can find it by squaring each Difference of the x-values and the Mean. you get:
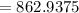
- Find the slope of the line
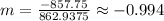
- Find the y-intercept with this formula:
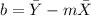
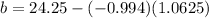
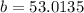
Therefore, the line in Slope-Intercept Form:
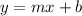
is the following:
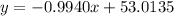
4. If:
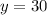
You can predict the vehicle weight by substituting that value into the equation found in Part 3, and solving for "x":
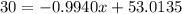
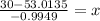
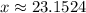
5. If a vehicle weighs 1500 pounds, then:
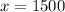
Then you can determine the expected city MPG of the vehicle by substituting this value into the equation and evaluating:
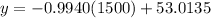
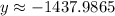
Hence, the answers are:
1.
2. It describes a negative correlation.
3.
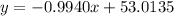
4.
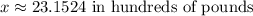
5.