Use the Pythagorean theorem to determine if the triangle is acute, obtuse or right triangle.
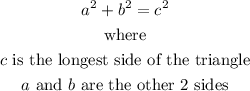
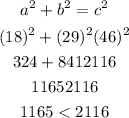

Since the sum of the square of the side of the two angles is less than the square of the longest side, then given the length of a triangle 18-29-46, the triangle is an obtuse triangle.