Question

Given the lengths of the sides of a triangle, determine if it is an acute, anobtuse, or a right triangle.

Answer 1

Use the Pythagorean theorem to determine if the triangle is acute, obtuse or right triangle.

`\begin{gathered} a^2+b^2=c^2 \\ \text{where} \\ c\text{ is the longest side of the triangle} \\ a\text{ and }b\text{ are the other 2 sides} \end{gathered}`
`\begin{gathered} a^2+b^2=c^2 \\ (18)^2+(29)^2\questeq(46)^2 \\ 324+841\questeq2116 \\ 1165\questeq2116 \\ 1165<2116 \end{gathered}`
`\begin{gathered} \text{IF} \\ a^2+b^2c^2 \\ \text{THEN, the triangle is an acute triangle} \\ \\ \text{IF} \\ a^2+b^2=c^2 \\ \text{THEN, the triangle is a right triangle} \end{gathered}`

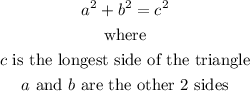
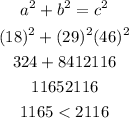
Since the sum of the square of the side of the two angles is less than the square of the longest side, then given the length of a triangle 18-29-46, the triangle is an obtuse triangle.