EXPLANATION
Given the following operation:
3/4 - 1/2*7/8
First, let's solve 1/2*7/8:
Multiply fractions: a/b* c/d = (a*c)/(b*d)
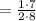
Multiply the numbers: 1*7 = 7
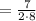
Multiply the numbers 2*8=16
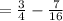
Now, we need the Least Common Multiplier of 4, 16:
The LCM of a, b is the samllest positive number that is divisible by both a and b:
Prime factorization of 4:
4 divides by 2 ---> 4= 2*2
2 is a primer number, therefore no further factorization is possible.
Prime factorization of 16:
Multiply each factor the greatest number of times it occurs in either 4 or 16
= 2*2*2*2
Multiply the numbers: 2*2*2*2 = 16
Adjust fractions based on LCM
For 3/4: multiply the denominator and numerator by 4
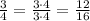
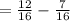
Since the denominators are equal, combine the fractions:
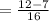
Subtract the numbers: 12-7 = 5