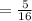Question

Step by step on how to solve 3/4 - 1/2 × 7/8

Answer 1

EXPLANATION

Given the following operation:

3/4 - 1/2*7/8

First, let's solve 1/2*7/8:

Multiply fractions: a/b* c/d = (a*c)/(b*d)

`=(1\cdot7)/(2\cdot8)`

Multiply the numbers: 1*7 = 7

`=(7)/(2\cdot8)`

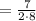
Multiply the numbers 2*8=16

`=(3)/(4)-(7)/(16)`

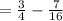
Now, we need the Least Common Multiplier of 4, 16:

The LCM of a, b is the samllest positive number that is divisible by both a and b:

Prime factorization of 4:

4 divides by 2 ---> 4= 2*2

2 is a primer number, therefore no further factorization is possible.

Prime factorization of 16:

Multiply each factor the greatest number of times it occurs in either 4 or 16

= 2*2*2*2

Multiply the numbers: 2*2*2*2 = 16

Adjust fractions based on LCM

For 3/4: multiply the denominator and numerator by 4

`(3)/(4)=(3\cdot4)/(3\cdot4)=(12)/(16)`
`=(12)/(16)-(7)/(16)`

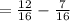
Since the denominators are equal, combine the fractions:

`=(12-7)/(16)`

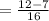
Subtract the numbers: 12-7 = 5

`=(5)/(16)`