Question

Find the area under the graph of f(x) = e-2ln(x) on the interval [1, 2]. (2 points)0.51.52.3331.75

Answer 1

Step-by-step explanation:

To solve the question, we will need to re-express the given function as follow:

`f(x)=e^(-2\ln (x))`

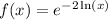
Will become

`f(x)=e^(-2\ln (x))=e^{\ln x^(-2)}`

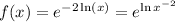
Thus

`f(x)=e^{\ln x^(-2)}=x^(-2)`

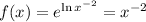
This simply means that we will find the area under the curve:

`f(x)=x^(-2)\text{ within the interval \lbrack{}1,2\rbrack}`

Thus

The area will be

`\int ^2_1f(x)dx=\int ^2_1x^(-2)dx`

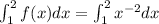
This will then be

`\lbrack(x^(-2+1))/(-2+1)\rbrack^2_1=\lbrack(x^(-1))/(-1)\rbrack^2_1`

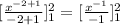
This will be simplified to give

`-\lbrack(1)/(x)\rbrack^2_1=-\lbrack((1)/(2))-((1)/(1))\rbrack=-1\lbrack-(1)/(2)\rbrack=(1)/(2)`

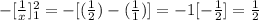
Therefore, the area under the curve will be

`(1)/(2)=0.5`

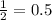
Thus, the answer is 0.5