Question

Farmer Ed has 2,000 meters of fencing, and wants to enclose a rectangular plot that borders on a river. If Farmer Ed does not fence the side along the river, what is the largest area that can be enclosed?

Answer 1

500,000cm²

Explanations:

The formula for calculating the perimeter of the fence is expressed as:

`P=2(l+w)`

where:

• L is the ,length, of the fencing

,

• W is the ,width ,of the fencing

If Farmer Ed does not fence the side along the​ river, the perimeter of the river will become;

`\begin{gathered} P=l+2w \\ 2000=l+2w \\ l=2000-2w \end{gathered}`

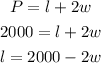
The area of the rectangular plot will be expressed as:

`A=lw`

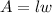
Substitute the expression for the length into the area to have:

`\begin{gathered} A=w(2000-2w) \\ A=2000w-2w^2 \end{gathered}`

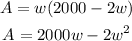
If the area of the plot is maximized, then dA/dw = 0. Taking the derivative will give:

`\begin{gathered} (dA)/(dw)=0 \\ 2000-4w=0 \\ 4w=2000 \\ w=(2000)/(4) \\ w=500m \end{gathered}`

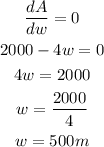
Calculate the length of the plot. Recall that:

`\begin{gathered} l=2000-2w \\ l=2000-2(500) \\ l=2000-1000 \\ l=1000m \end{gathered}`

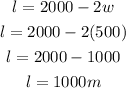
Determine the largest area that can be​ enclosed

`\begin{gathered} A=lw \\ A=500m*1000m \\ A=500,000m^2 \end{gathered}`

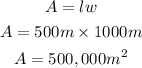
Hence the largest area that can be​ enclosed is 500,000cm²