The system of equations:
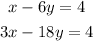
This comes from the fact that if we multiply the first equation by 3 then we have:
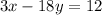
But this clearly contradicts the second one. Then the system has no solutions.
a.
To find a system with one solution we only have to change one of the coefficients of the equation. If we change the first x coefficient from 1 to 2. then we have the system:
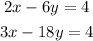
which has one solution.
b.
To find a system with an infinite number of solutions we can change the constant of the second equation to 12, then:

then if we multiply the first by 3 then we have the second one, therefore the equations are the same and the system will have and infinite number os solutions.