Question

Find two numbers whose sum is 256, but whose product is a maximum?

Answer 1

The two numbers are 128 and 128

Step-by-step explanation

Let the two numbers be x and y.

We have that:

`\begin{gathered} x+y=256 \\ x\cdot y=A \end{gathered}`

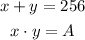
where A is a maximum.

From the first equation:

`x=256-y`

Substitute that into the second equation:

`\begin{gathered} (256-y)\cdot y=A \\ \Rightarrow256y-y^2=A \\ \Rightarrow y^2-256y+A=0 \end{gathered}`

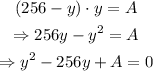
The equation above is a quadratic equation in the general form:

`ax^2+bx+c=0`

The parabola is downward facing and so, its vertex will be the maximum.

We can find the vertex (x, y) of the parabola by using:

`x=(-b)/(2a)`

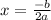
In the case given, the vertex can be found by using:

`\begin{gathered} y=(-(-256))/(2(1))=(256)/(2) \\ y=128 \end{gathered}`

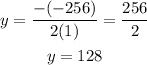
Recall that:

`x=256-y`

Therefore, we have that:

`\begin{gathered} x=256-128 \\ x=128 \end{gathered}`

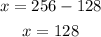
Hence, the two numbers are 128 and 128.