The formula to find how many different ways are there to choose a subgroup of r things from a group of n things is
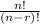
Here, you have 7 trophies and you want to choose 4 of them, so you have

So there are 840 ways to choose your 4 trophies out of the 7 you have.