We are given the following information
f(-1) = 16 and f(5) = -8
Which means that
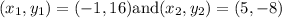
a. Find the distance between these points
Recall that the distance formula is given by
![d=\sqrt[]{\mleft({x_2-x_1}\mright)^2+\mleft({y_2-y_1}\mright)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/wk0274bc8to4x64qfz58fb6i4btzelzdis.png)
Let us substitute the given points into the above distance formula
![\begin{gathered} d=\sqrt[]{({5_{}-(-1)})^2+({-8_{}-16_{}})^2} \\ d=\sqrt[]{({5_{}+1})^2+({-24_{}})^2} \\ d=\sqrt[]{({6})^2+({-24_{}})^2} \\ d=\sqrt[]{36^{}+576^{}} \\ d=\sqrt[]{612} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/jbdwy8w6i72r0duk05h4trrvxwiemfeqsp.png)
Therefore, the distance between these points is √612 = 24.738
b. Find the midpoint between these points
Recall that the midpoint formula is given by
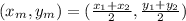
Let us substitute the given points into the above midpoint formula
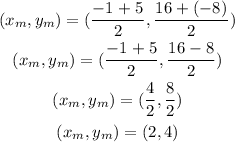
Therefore, the midpoint of these points is (2, 4)
c. Find the slope between these points
Recall that the slope is given by
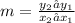
Let us substitute the given points into the above slope formula
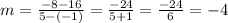
Therefore, the slope of these points is -4.