Question

Let f(-1)=16 and f(5) = -8a. Find the distance between these pointsb. Find the midpoint between these pointsc. Find the slope between these points

Answer 1

We are given the following information

f(-1) = 16 and f(5) = -8

Which means that

`(x_1,y_1)=(-1,16)\text{and}(x_2,y_2)=(5,-8)`

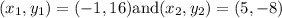
a. Find the distance between these points

Recall that the distance formula is given by

`d=\sqrt[]{\mleft({x_2-x_1}\mright)^2+\mleft({y_2-y_1}\mright)^2}`

Let us substitute the given points into the above distance formula

`\begin{gathered} d=\sqrt[]{({5_{}-(-1)})^2+({-8_{}-16_{}})^2} \\ d=\sqrt[]{({5_{}+1})^2+({-24_{}})^2} \\ d=\sqrt[]{({6})^2+({-24_{}})^2} \\ d=\sqrt[]{36^{}+576^{}} \\ d=\sqrt[]{612} \end{gathered}`

Therefore, the distance between these points is √612 = 24.738

b. Find the midpoint between these points

Recall that the midpoint formula is given by

`(x_m,y_m)=((x_1+x_2)/(2),(y_1+y_2)/(2))`

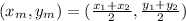
Let us substitute the given points into the above midpoint formula

`\begin{gathered} (x_m,y_m)=(\frac{-1_{}+5_{}}{2},\frac{16_{}+(-8)_{}}{2}) \\ (x_m,y_m)=(\frac{-1_{}+5}{2},\frac{16_{}-8}{2}) \\ (x_m,y_m)=((4)/(2),(8)/(2)) \\ (x_m,y_m)=(2,4) \end{gathered}`

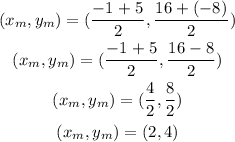
Therefore, the midpoint of these points is (2, 4)

c. Find the slope between these points

Recall that the slope is given by

`m=(y_2−y_1)/( x_2−x_1)`

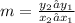
Let us substitute the given points into the above slope formula

`m=(-8-16)/(5-(-1))=(-24)/(5+1)=(-24)/(6)=-4`

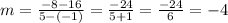
Therefore, the slope of these points is -4.