We have a problem that can be solved with a system of equations.
First we need to identify the equations of the system.
We have two unknown variables, the number of adult's tickets sold and the number of children's tickets sold. Let's call them:
- number of adult's tickets sold: x
- number of children's tickets sold: y.
The total number of tickets sold, 5600, is the sum of these:
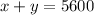
And since the prices are 27.25 (adult) and 12.00 (children), the total revenue (117311.50) will be the sum of these prices multiplyied by the number of tickets of each of them:
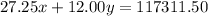
So, the system of equations is:
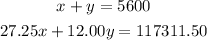
Since we want y the number of children's tickets sold, we can solve for the other varible, x, in one equation, and substitute into the other.
Solving in the first equation, we have:
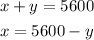
And substituting into the other:

Since y is the number of children's tickets sold, then the number of children's tickets sold is 2314.