We will find the vertex of the parabola as follows:
*Given a quadratic function of the form:

We will have that the vertex is given by:
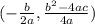
So, for the function given we will have the following vertex:
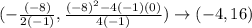
So, the vertex for the function is given by the ordered pair (-4, 16).
We will have that the equation of the axis of symmetry is given by:
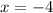
So, the axis of symmetry is x = -4.
We will determine the x-intercepts as follows:
![-x^2-8x=0\Rightarrow x=\frac{-(-8)\pm\sqrt[]{(-8)^2-4(-1)(0)}}{2(-1)}](https://img.qammunity.org/2023/formulas/mathematics/high-school/7p2kyt22tou49bjixumknm64g2mtsxir5f.png)

So, we will have that the x-intercepts are located at x = -8 & x = 0.
From the previous point we can see that the point (0, 0) belongs to the parabola, thus the y-intercept is y = 0.