Question

What are the solutions of the equation 0 equals x ^ 2 + 3x - 10

Answer 1

The given expression is :

`0=x^2+3x-10`

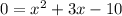
Factorize the expression :

`\begin{gathered} 0=x^2+3x-10 \\ x^2+3x-10=0 \end{gathered}`

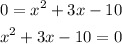
Find the pair of number such that : the product of two numbers are equal = (-10)

and thier summation is equal to 3

i.e. 5 x ( -2) = -10 and 5 + (-2) = 3

So,

`\begin{gathered} x^2+3x-10=0 \\ x^2+5x-2x-10=0 \end{gathered}`

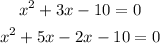
Take x common from the first two terms and (-2) from last two terms :

`\begin{gathered} x^2+5x-2x-10=0 \\ x(x+5)-2(x+5)=0 \\ \text{Now, take (x+5) common :} \\ (x-2)(x+5)\text{ =0} \end{gathered}`

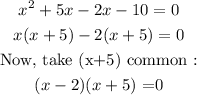
Now equate each factor with zero :

`\begin{gathered} (x-2)(x+5)=0 \\ x-2=0\Rightarrow x=2 \\ x+5=0\Rightarrow x=-5 \end{gathered}`

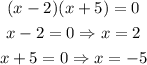
Answer : C) x = -5, 2