Question

A student bought a calculator and a textbook for a course in algebra. He told his friend that the total cost was $165 (without tax) and thatthe calculator cost $25 more than thrice the cost of the textbook. Whatwas the cost of each item? Let x = the cost of a calculator andy = the cost of the textbook. The corresponding modeling system is { x = 3y + 25x + y =Solve the system by using the method of= 165substitution

Answer 1

We know that the calculator price (x) was 25 more than 3 times the price of the textbook (y).

This can be represented as:

`x=3y+25`

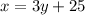
We also know that the sum of the prices of the two items is equal to $165:

`x+y=165`

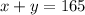
We have to solve this system of equations with the method of substitution.

We can use the first equation, as we have already clear the value of x, to substitute x in the second equation and then solve for y:

`\begin{gathered} x+y=165 \\ (3y+25)+y=165 \\ 4y+25=165 \\ 4y=165-25 \\ 4y=140 \\ y=(140)/(4) \\ y=35 \end{gathered}`

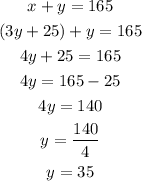
With the value of y we can calculate x using the first equation:

`\begin{gathered} x=3y+25 \\ x=3\cdot35+25 \\ x=105+25 \\ x=130 \end{gathered}`

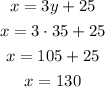
Answer: the solution as ordered pair is (x,y) = (130, 35)