For conic section of the form:

The Ends of the Lactus Rectum is given as:
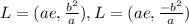
The e in the equation above is the Eccentricity of the Hyperbola.
This can be obtained by the formula:
![e=\frac{\sqrt[]{a^2+b^2}}{a}](https://img.qammunity.org/2023/formulas/mathematics/high-school/w11xtyyzluuqx2mv2ktmjksqfxmfy8v2d1.png)
Thus, comparing the standard form of the conic with the given equation, we have:
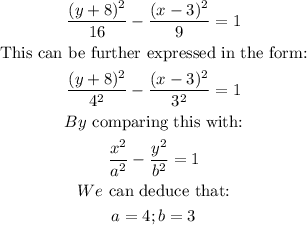
Then, we need to obtain the value of the Eccentiricity, e.
![\begin{gathered} e=\frac{\sqrt[]{a^2+b^2}}{a} \\ e=\frac{\sqrt[]{4^2+3^2}}{4} \\ e=\frac{\sqrt[]{16+9}}{4} \\ e=\frac{\sqrt[]{25}}{4}=(5)/(4) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/zlfl1pmfvndg3dmedqo17d5987d93btxip.png)
Hence, the coordinate of the ends of the each lactus rectum is:
