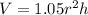Question

The volume V of a cone varies jointly as the square of the radius of the base,r, and the height, h. Find the equation of the joint variation if v =285, r=4, and h = 17.

Answer 1

V = 1.05r²h

Step-by-step explanation:

The expression ''the volume V of a cone varies jointly as the square of the radius of the base,r, and the height, h'' can be represented as:

`V=k\cdot r^2\cdot h`

Where the k is a constant.

So, replacing V = 285, r = 4, and h = 17, we get:

`285=k\cdot4^2\cdot17`

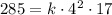
Solving for k, we get:

`\begin{gathered} 285=k\cdot16\cdot17 \\ 285=k\cdot272 \\ (285)/(272)=(k\cdot272)/(272) \\ 1.05=k \end{gathered}`

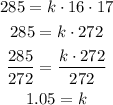
So, the equation of the joint variation is:

`V=1.05r^2h`