Question

A car was valued at $32,000 in the year 1995. The value depreciated to $14,000 by the year 2001.A) What was the annual rate of change between 1995 and 2001?T =Round the rate of decrease to 4 decimal places.B) What is the correct answer to part A written in percentage form?T =%.C) Assume that the car value continues to drop by the same percentage. What will the value be in the year2005 ?value = $Round to the nearest 50 dollars.

Answer 1

Givn:

Value of the car in 1995 = $32,000

Value of the car in 2001 = $14,000

Let's solve for the following:

• (A). What was the annual rate of change between 1995 and 2001?

Apply the exponential decay formula:

`f(t)=a(1-r)^t`

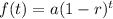
Where:

• t is the number of years between 2001 and 1995 = 2001 - 1995 = 6

,

• a is the initial value = $32000

,

• r is the rate of decay.

,

• f(t) is the present value

Thus, we have

`\begin{gathered} 14000=32000(1-r)^6 \\ \end{gathered}`

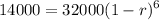
Divide both sides by 32000:

`\begin{gathered} (14000)/(32000)=(32000(1-r)^6)/(32000) \\ \\ 0.4375=(1-r)^6 \end{gathered}`

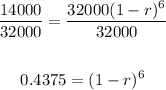
Take the 6th root of both sides:

`\begin{gathered} \sqrt[6]{0.4375}=\sqrt[6]{(1-r)^6} \\ \\ 0.87129=1-r \end{gathered}`

Solving further:

`\begin{gathered} r=1-0.87129 \\ \\ r=0.1287 \\ \\ r=0.1287*100=12.87\text{ \%} \end{gathered}`

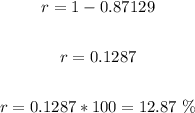
Therefore, the rate of change between 1995 and 2001 is 0.1287

• (B). What is the correct answer to part A written in percentage form?

In percentage form, the rate of change is 12.87 %

• (C),. Assume that the car value continues to drop by the same percentage. What will the value be in the year 2005?

We have the equation which represents this situation below:

`f(t)=32000(1-0.1287)^t`

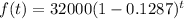
Here, the value of t will be the number of years between 1995 and 2005.

t = 2005 - 1995 = 10

Now, substitute 10 for t and solve for f(10):

`\begin{gathered} f(10)=32000(1-0.1287)^(10) \\ \\ f(10)=32000(0.8713)^(10) \\ \\ f(10)=32000(0.25216) \\ \\ f(10)=8069.14\approx8100 \end{gathered}`

Therefore, the value in the year 2005 rounded to the nearest 50 dollars is $8100

ANSWER:

• (a). 0.1287

,

• (b). 12.87%

,

• (c). $8100