Question

Simplify the expression 3^2/ 3^1/4 to demonstrate the quotient of powers property. Show any intermittent stepsthat demonstrate how you arrived at the simplified answer.

Answer 1

We are given a quotinet of two power expressions to be used to demonstrate the quotient property of powers:

`\frac{3^2}{3^{(1)/(4)}}=3^2\cdot3^{-(1)/(4)}=3^{((8)/(4)-(1)/(4))}=3^{(7)/(4)}`

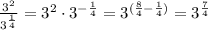
ANother way of doing it is to represent 3^2 as 3 to the power 8/4 so as to have the same radical expression.

Recall that fractional exponents are associated with radicals, and in this case the power "1/4" represents the fourth root of the base "3". That is:

`3^{(1)/(4)}=\sqrt[4]{3}`

So we also write 3^2 with fourth root when we express that power "2 = 8/4":

`3^2=3^{(8)/(4)}=\sqrt[4]{3^8}`

So now, putting that quotient together we have:

`\frac{\sqrt[4]{3^8}}{\sqrt[4]{3}}=\sqrt[4]{(3^8)/(3)}=\sqrt[4]{3^7}=3^{(7)/(4)}`

So we see that we arrived at the same expression "3 to the power 7/4"

in both cases. One was using the subtraction of the powers as the new power for the base 3, and the other one was using the radical form of fractional powers.