We are given a quotinet of two power expressions to be used to demonstrate the quotient property of powers:
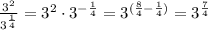
ANother way of doing it is to represent 3^2 as 3 to the power 8/4 so as to have the same radical expression.
Recall that fractional exponents are associated with radicals, and in this case the power "1/4" represents the fourth root of the base "3". That is:
![3^{(1)/(4)}=\sqrt[4]{3}](https://img.qammunity.org/2023/formulas/mathematics/college/ui0q85kc9r0wifbvou1iytmyw57bmgkge4.png)
So we also write 3^2 with fourth root when we express that power "2 = 8/4":
![3^2=3^{(8)/(4)}=\sqrt[4]{3^8}](https://img.qammunity.org/2023/formulas/mathematics/college/ux43sxgm5l2s90ifcuy4oxphdf5vxwzqh4.png)
So now, putting that quotient together we have:
![\frac{\sqrt[4]{3^8}}{\sqrt[4]{3}}=\sqrt[4]{(3^8)/(3)}=\sqrt[4]{3^7}=3^{(7)/(4)}](https://img.qammunity.org/2023/formulas/mathematics/college/3f3z0d6j7rdt2zrgoizgcqvk2lm0tqjoi4.png)
So we see that we arrived at the same expression "3 to the power 7/4"
in both cases. One was using the subtraction of the powers as the new power for the base 3, and the other one was using the radical form of fractional powers.