Given:
3x - 5y = 18
To graph this line, rewrite the equation in slope-intercept form:
y = mx + b
Where m is the slope and b is the y-intercept.
Subtract 3x from both sides:
3x - 3x - 5y = -3x + 18
-5y = -3x + 18
Divide all terms by -5:
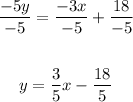
Thus, the slope intercept form of the equation is:
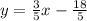
Any line can be graphed using two or more points.
Let's determine two points on the line.
Input 6 for x and solve for y:
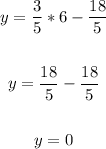
Also, the y-intercept is:
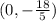
convert the fraction to decimal:
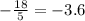
Thus, we have the points:
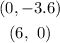
x y
0 -3.6
6 0
Mark the points on a graph and make a straight line that passes through the points.
The graph is attached below: