Question

Graph the line 3x - 5y = 18

Answer 1

Given:

3x - 5y = 18

To graph this line, rewrite the equation in slope-intercept form:

y = mx + b

Where m is the slope and b is the y-intercept.

Subtract 3x from both sides:

3x - 3x - 5y = -3x + 18

-5y = -3x + 18

Divide all terms by -5:

`\begin{gathered} (-5y)/(-5)=(-3x)/(-5)+(18)/(-5) \\ \\ y=(3)/(5)x-(18)/(5) \end{gathered}`

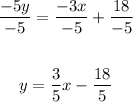
Thus, the slope intercept form of the equation is:

`y=(3)/(5)x-(18)/(5)`

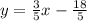
Any line can be graphed using two or more points.

Let's determine two points on the line.

Input 6 for x and solve for y:

`\begin{gathered} y=(3)/(5)\ast6-(18)/(5) \\ \\ y=(18)/(5)-(18)/(5) \\ \\ y=0 \end{gathered}`

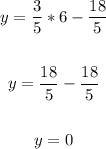
Also, the y-intercept is:

`(0,-(18)/(5))`

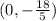
convert the fraction to decimal:

`-(18)/(5)=-3.6`

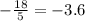
Thus, we have the points:

`\begin{gathered} (0,-3.6) \\ (6,\text{ 0)} \end{gathered}`

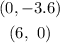
x y

0 -3.6

6 0

Mark the points on a graph and make a straight line that passes through the points.

The graph is attached below: