hello
to solve this question, we simply need to apply the formula of area of a segment
the formula is given as
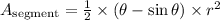
let's write out the variables given in the question
![\begin{gathered} \theta=60^0 \\ r=5\operatorname{cm} \end{gathered}]()
we can now input those values into the equation
![\begin{gathered} A_{\text{segment}}=(1)/(2)*(\theta-\sin \theta)* r^2 \\ A_{\text{segment}}=(1)/(2)*(60-\sin 60)*5^2 \\ A_{\text{segment}}=(1)/(2)*(60-0.8660)*25 \\ A_{\text{segment}}=(1)/(2)*1478.35 \\ A_{\text{segement}}=739.175\operatorname{cm}^2 \end{gathered}]()
to get the value of the area of the shaded region,
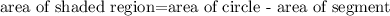
let's calculate the area of the circle
![undefined]()