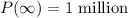Question

We estimate that the population of a certain, in t years will be given byp (t) = (2t² + 75) / (2t² + 150) million habitantsAccording to this hypothesis:What is the current population?What will it be in the long term?Sketch the population graph

Answer 1

Given that the population can be represented by the equation;

`P(t)=(2t^2+75)/(2t^2+150)`

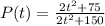
The current population (Initial population) is the population at time t=0;

Substituting;

`t=0`
`\begin{gathered} P(0)=(2t^2+75)/(2t^2+150)=(2(0)^2+75)/(2(0)^2+150)=(75)/(150) \\ P(0)=0.5\text{ million} \end{gathered}`

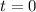
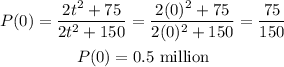
Therefore, the current population of the habitat is;

`0.5\text{ million}`

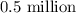
The long term population would be the population as t tends to infinity;

`\begin{gathered} \lim _(t\to\infty)P(t)=(2t^2+75)/(2t^2+150)=(2(\infty)^2+75)/(2(\infty)^2+150)=(\infty)/(\infty) \\ \lim _(t\to\infty)P(t)=(4t)/(4t)=1 \end{gathered}`

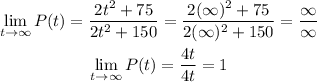
Therefore, the long term population of the habitat is;

`P(\infty)=1\text{ million}`