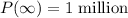Given that the population can be represented by the equation;
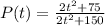
The current population (Initial population) is the population at time t=0;
Substituting;

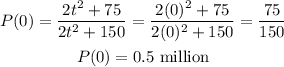
Therefore, the current population of the habitat is;
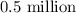
The long term population would be the population as t tends to infinity;
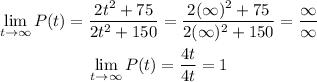
Therefore, the long term population of the habitat is;