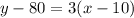We know that the line passes through the points (10,130) and (20,200).
First, we have to find the slope with the following formula

Where,

Replacing these coordinates, we have
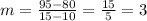
The slope is 7.
Now, we use one point, the slope, and the point-slope formula to find the equation
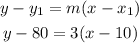
Therefore, the point-slope form of the line is