Solution:
The reciprocal identities of trigonometry include the identities below
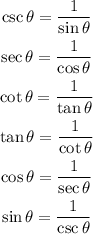
The quotient identity include the identities below
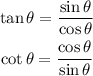
The sum formula of trigonometric identity include
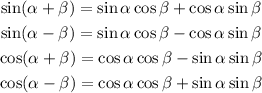
The double-angle formula is given below as
Hence,
The final answer is QUOTIENT IDENTITY