Question

1) To win the small county lottery, one must correctly select 3 numbers from 30 numbers. The order in which the selection is made does not matter. How many different selections are possible?

Answer 1

This problem involves combination with taken n Items taken r at a time

The formula for this combination is :

`nC_r=(n!)/((n-r)!r!)`

Where n is the total number of items

and r is the objects taken at a time

The factorial, n! denotes n x (n-1) x (n-2) x (n-3) x ... x (1)

For example :

2! = 2 x 1 = 2

3! = 3 x 2 x 1 = 6

4! = 4 x 3 x 2 x 1 = 24

Now from the given problem :

we have n = 30 numbers

r = selection of 3

Then the formula will be :

`30C_3=(30!)/((30-3)!*3!)`

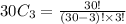
Simplifying :

27 up to 1 will be cancelled from numerator and the denominator..

Evaluating the expression will be :

24360/6 = 4060

The answer is 4060