We have the following vertices given:
A(-3,6), B=(6,0), C(9,-9), D=(0,-3)
a) We can begin find the distance between two points using this formula:
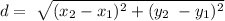
For this case we need to find the distance between AD and BC and using the formula given we have:


We see that both distances are equal. Now we can calculate the slopes for AD and BC and we got using this formula:
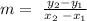
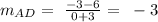
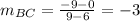
Then we can conclude that the quadrilateral is a paralellogram because it has one pair of opposite sides that both congruent and parallel
b) For this problem is not a rhombus because not all the distances AB, AC, AD, BC and CD are equal