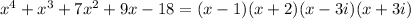To find the zeros of the polynomial given, we will first have to find some simpler zeros first then factor the polynomial so we can use the quadratic equation.
Since we can assume this question is to be solved without external tools, it is likely that two of the roots are simple ones.
So, we can try to use the rational root theorem to find these simpler ones.
Since the leading coefficient is 1 and the constant term is -18, if there are rational roots, they can be written as a fraction of a factor of -18 divided by a factor of 1.
The only factor of 1 is 1, so we now that if there are rational roots, they have to have denominator equal to 1.
The factors of 18 are 1, 2, 3, 6, 9 and 18.
Also, we have to consider the possibilities of positive and negative.
It is easier to test the lower ones, so let's start by testing 1/1 and -1/1. For either to be a zero, the polynomial has to result in 0:
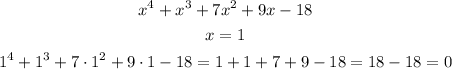
So, x = 1 is a zero of the polynomial.
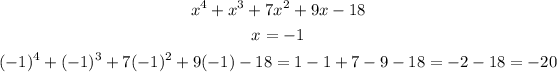
So, x = -1 is not a zero.
Now, let's try the next factor, 2/1 and -2/1:
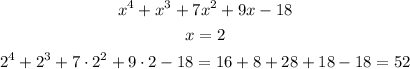
So, x = 2 is not a zero.
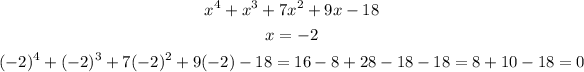
So, x = -2 is also a zero of the polynomial.
We could continue, by we only need 2 zeros, so this is enough.
Now we know x = 1 and x = -2 are zeros of the polynomial, we can use synthetic division to factor the polynomial:
1 | 1 1 7 9 -18
| 1 2 9 18
| 1 2 9 18 0
Using the last line, we have that the remainder is 0 and the quotient is:
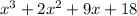
So, we have that:

Now, we can use synthetic division again on the quotient, but now use the other zero, x = -2:
-2 | 1 2 9 18
| -2 0 -18
| 1 0 9 0
Since x = -2 is a zero, we also got a remainder of 0, and the quotient is:
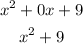
So, we can rewrite the polynomial as:

Now, we can just find the zeros of the remainer factor, x² + 9, so:
![\begin{gathered} x^2+9=0 \\ x^2=-9 \\ x=\pm\sqrt[]{-9} \\ x=\pm\sqrt[]{9}\sqrt[]{-1} \\ x=\pm3i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/h6nijhreuodld497nn3pzuwhor6tgeuktt.png)
This means that the complex zeros of the given polynomial are:
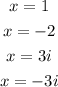
And the factored usinf complex factors is: