Answer:
(A) 7/6 pi /s^2
(B) 4.145 m/s^2
(C) 119pi/200 m/s^2
Step-by-step explanation:
Part A.
The angular acceleration is given by
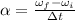
where wf is the initial angular velocity and wi is the final angular velocity and t is the time interval.
Now, we are given the angular velocity is given in rpm and we have to convert it into radians/sec .
150 rpm = 150 x 2pi / 60 min = 5 pi rad/ sec
290 rpm = 290 x 2pi / 60 min = 29/ 3 pi rad/ sec
Now we are in the position to find the angular acceleration
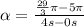
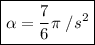
which is our answer!
Part B.
The radial acceleration is given by
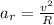
where v is the velocity of the object (moving in a circle) and R is the radius of the circle.
Now,
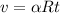
putting in the values of alpha, R and t = 1.1 s gives
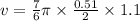
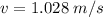
therefore,
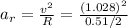
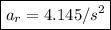
which is our answer!
Part C.
Here we have to relationship between angular and tangential acceleration:
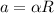
where r is the radius of the circle.
Since R = 0.51/2 m, we have
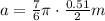
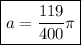
which is our answer!
Hence, to summerise
(A) 7/6 pi /s^2
(B) 4.145 m/s^2
(C) 119pi/200 m/s^2