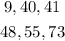From the Pythagorean Theorem, if a, b and c are the sides of a right triangle, with c being the longest side, then:
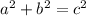
Or, equivalently:
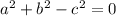
Find the corresponding values of the second expression for each case. If the result is equal to 0, then those are the sides of a right triangle:
9, 40 and 41
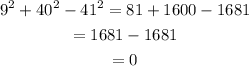
Then, these are the sides of a right triangle.
11, 60 and 62
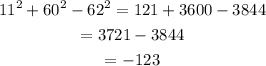
Then, these are not the sides of a right triangle.
48, 55 and 73
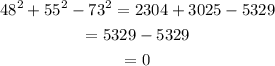
Then, these are the sides of a right triangle.
Therefore, from the given sets of numbers, the ones that correspond to lengths of sides of a rigtr triangle, are: