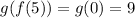Starting from the first question, we want:
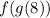
Let's start from the inside part:
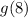
Since the inside of "g" is 8, this means we need to check for the row with x = 8, thay is, "8" in the column "x". Finding this row, we check the value in this row and column "g", which is "4".
This means that:
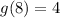
Now, we can substitute this back in:
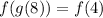
And we can do similarly. We check the row which has "4" in the "x" column and see the corresponding value in column "f". We can see that it is also "4", so, the answer for the first is:
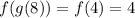
Lastly, for the second, we do the same thing, the inside part is:
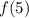
So, we got to line x = 5 and check column "f". It is 0, so:
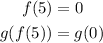
Now, we check row x = 0 and column "g" to find "9", so:
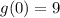
Thus, the answer for the second is: