ANSWERS
(a) 3.58 x 10⁶ N/m
(b) 5.8 x 10⁶ J
Step-by-step explanation
Given:
• The mass of the object hanging from the spring, m = 4.00 x 10⁵ kg
Find:
• (a), The force constant the springs should have to make the object oscillate with a period of 2.10 s
,
• (b), The energy stored in the springs for a 1.80 m displacement from equilibrium.
(a) The period of an object in a spring is,
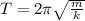
Where m is the mass of the object and k is the spring constant.
We want to find k for T = 2.10 s, so we have to solve this equation for k, which gives us,

Replace the known values and solve,
![k=4\cdot10^5\cdot(4\pi^2)/((2.1)^2)\approx3,580,808.85N/m\approx3.58\cdot10^^6N/m]()
Hence, the force constant is 3.58 x 10⁶ N/m.
(b) The energy stored in a spring with force constant k when the mass is displaced x meters from equilibrium is,
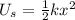
Replace the known values and solve to find the energy stored in this spring,

Hence, the energy stored in the spring for a 1.80 m displacement from equilibrium is 5.8 x 10⁶ J.