Given: The sum of the catheters in a triangle is 27 cm
To Determine: The area of the triangle
Solution
Please note the below
Let the first cathetus be x, then the second cathetus would be
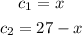
For the second right triangle
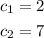
Since the two right triangles are corresponding to each other, then the ratio of their cathethers are equal
Therefore
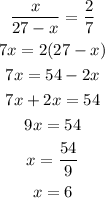
So, the cathethers for the first right triangle would be
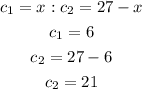
Note that the catheters formed the base and the height of the first triangle. The area of a triangle can be calculated using the formula below
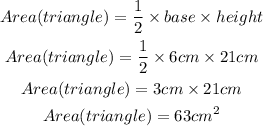
Hence, the area of the first triangle is 63cm²