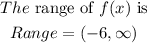Question

I answered a problem for my prep guide, I just need to know if I’m correct or not. And I would like it to be answered as well just to make sure that I did everything correctly

Answer 1

Notice that,

`f(x)=3^(x-1)-6=3^x\cdot3^(-1)-6=(3^x)/(3)-6`

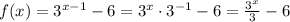
And there are no restrictions for the values that x can take. The domain is the whole set of real numbers.

Now, we need to check for the limits when x->+/- infinite, as follows:

`\begin{gathered} \lim _(x\to\infty)3^x=\infty \\ \lim _(x\to-\infty)3^x=\lim _(x\to\infty)(1)/(3^x)=0 \end{gathered}`

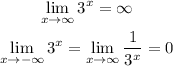
Then, the range of 3^x is (0, infinite).

Finally, we can get the range of function f(x):

`\lim _(x\to\infty)f(x)=(1)/(3)(\lim _(x\to\infty)3^x)-6=(1)/(3)\infty-6=\infty`
`\lim _(x\to-\infty)f(x)=(1)/(3)(\lim _(x\to-\infty)3^x)-6=(1)/(3)\cdot0-6=-6`

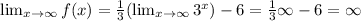
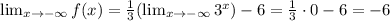
Then,

`\begin{gathered} The\text{ range of }f(x)\text{ is} \\ Range=(-6,\infty) \end{gathered}`