Question

Could someone help me with this math problem? thanks a lot if you do (:

Answer 1

We will have the following:

First, we determine the slope of the linear relationship:

`m=(320-380)/(2.75-2.5)\Rightarrow m=-240`

a) Now, using this information and one point (2.50, 380) we will replace in the general equation for a linear function, that is:

`\begin{gathered} N(p)-y_1=m(p-x_1)\Rightarrow N(p)-380=-240(p-2.5) \\ \\ \Rightarrow N(p)-380=-240p+600 \\ \\ \Rightarrow N(p)=-240p+980 \end{gathered}`

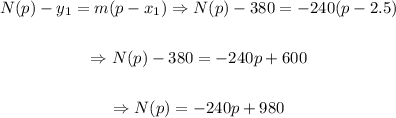
So, the equation is:

`N(p)=-240p+980`

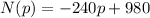
b) We determine the revenue function as follows:

`\begin{gathered} R(p)=pN(p)\Rightarrow R(p)=p(-240p+980) \\ \\ \Rightarrow R(p)=-240p^2+980p \end{gathered}`

So, the equation of revenue is:

`R(p)=-240p^2+980p`

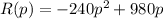
c) We determine the critical points of the revenue:

`\begin{gathered} R^(\prime)(p)=-480p+980=0\Rightarrow480p=980 \\ \\ \Rightarrow p=(49)/(24)\Rightarrow p\approx2.04 \end{gathered}`

So, the price that maximizes revenue is approximately $2.04.

The maximum revenue will be:

`\begin{gathered} R(2.04)=-240(2.04)^2+980(2.04)\Rightarrow R(2.04)=1000.416... \\ \\ \Rightarrow R(2.04)\approx1000.42 \end{gathered}`

So, the maximum revenue is approximately $1000.42.