We will have the following:
First, we determine the slope of the linear relationship:
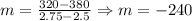
a) Now, using this information and one point (2.50, 380) we will replace in the general equation for a linear function, that is:
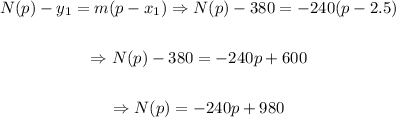
So, the equation is:
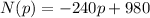
b) We determine the revenue function as follows:
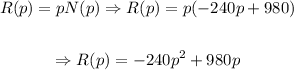
So, the equation of revenue is:
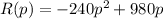
c) We determine the critical points of the revenue:
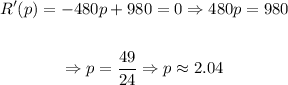
So, the price that maximizes revenue is approximately $2.04.
The maximum revenue will be:
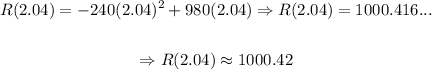
So, the maximum revenue is approximately $1000.42.