The situation can be represented by a linear function, which is represented by the following expression:
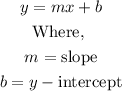
Since he increased the number of cards by a constant amount each week, that means we have proportionality:
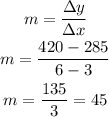
Then, by the slope-point form of the line, we can find the equation and then substitute x=0.
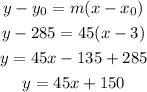
Substituting, x=0.
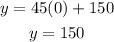
At the beginning of the collection, he has 150 cards.