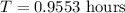Question

A swimmer is 1 mile from the closest point on a straight shoreline. She needs to reach her house located 4miles down shore from the closest point. If she swims at 3 mph and runs at 6 mph, how far from her house should she come ashore so as to arrive at her house in the shortest time?

Answer 1

Let's draw a diagram of this problem.

ABC is the shore.

D to A is 1 miles (given).

A to C is 4 miles (given).

If we let AB = x, then BC would be "4 - x".

Now, using pythgorean theorem, let's find BD:

`\begin{gathered} AB^2+AD^2=BD^2 \\ x^2+1^2=BD^2 \\ BD=\sqrt[]{1+x^2} \end{gathered}`

We know

`D=RT`

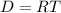
Where

D is distance

R is rate

T is time

Swimmer needs to go from D to B at 3 miles per hour. Thus, we can say:

`\begin{gathered} D=RT \\ T=(D)/(R) \\ T=\frac{\sqrt[]{1+x^2}}{3} \end{gathered}`

Next part, swimmer needs to go from B to C at 6 miles per hour. Thus, we can say:

`\begin{gathered} D=RT \\ T=(D)/(R) \\ T=(4-x)/(6) \end{gathered}`

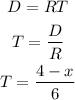
So, total time would be:

`T=\frac{\sqrt[]{1+x^2}}{3}+(4-x)/(6)`

We want to find the shortest possible time. From calculus we know that to find the shortest possible time, we need to differentiate the function T, set it equal to 0 to find the critical points and then use that point in the function T to find the shortest possible time.

Let's differentiate the function T:

`\begin{gathered} T=\frac{\sqrt[]{1+x^2}}{3}+(4-x)/(6) \\ T=(1)/(3)(1+x^2)^{(1)/(2)}+(4)/(6)-(1)/(6)x \\ T=(1)/(3)(1+x^2)^{(1)/(2)}+(2)/(3)-(1)/(6)x \\ T^(\prime)=((1)/(2))(1)/(3)(1+x^2)^{-(1)/(2)}\lbrack(d)/(dx)(1+x^2)\rbrack-(1)/(6) \\ T^(\prime)=(1)/(6)(1+x^2)^{-(1)/(2)}(2x)-(1)/(6) \\ T^(\prime)=\frac{2x}{6(1+x^2)^{(1)/(2)}}-(1)/(6) \\ T^(\prime)=\frac{x}{3\sqrt[]{1+x^2}}-(1)/(6) \end{gathered}`

Now, we find the critical point:

`\begin{gathered} T^(\prime)=\frac{x}{3\sqrt[]{1+x^2}}-(1)/(6) \\ T^(\prime)=0 \\ \frac{x}{3\sqrt[]{1+x^2}}-(1)/(6)=0 \\ \frac{x}{3\sqrt[]{1+x^2}}=(1)/(6) \\ \text{Cross Multiplying:} \\ 6x=3\sqrt[]{1+x^2} \\ \text{Square both sides:} \\ (6x)^2=(3\sqrt[]{1+x^2})^2 \\ 36x^2=9(1+x^2) \\ 36x^2=9+9x^2 \\ 36x^2-9x^2=9 \\ 27x^2=9 \\ x^2=(9)/(27) \\ x=\frac{\sqrt[]{9}}{\sqrt[]{27}} \\ x=\frac{3}{3\sqrt[]{3}} \\ x=\frac{1}{\sqrt[]{3}} \end{gathered}`

Plugging this value into the equation of T, we get:

`\begin{gathered} T=\frac{\sqrt[]{1+x^2}}{3}+(4-x)/(6) \\ T=\frac{\sqrt[]{1+(\frac{1}{\sqrt[]{3}})^2}}{3}+\frac{4-\frac{1}{\sqrt[]{3}}}{6} \\ T=\frac{\sqrt[]{1+(1)/(3)}}{3}+\frac{4-\frac{1}{\sqrt[]{3}}}{6} \\ T=\frac{\sqrt[]{(4)/(3)}}{3}+\frac{4-\frac{1}{\sqrt[]{3}}}{6} \\ T=\frac{\frac{2}{\sqrt[]{3}}}{3}+\frac{4-\frac{1}{\sqrt[]{3}}}{6} \\ T=\frac{2}{3\sqrt[]{3}}+\frac{4-\frac{1}{\sqrt[]{3}}}{6} \end{gathered}`

Now, we can use the calculator to find the approximate value of T to be:

T = 0.9553 hours

This is the optimized time.

Converting to approximate minutes, it will be:

57.32 minutes

Answer:
`T=0.9553\text{ hours}`