Given data:
The first end point of the diameter is (-14, 1).
The second end point of the diameter is (-10, 9).
The centre of the circel is,
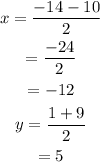
The diameter of the circle is,
![\begin{gathered} d=\sqrt[]{(-10+14)^2+(9-1)^2} \\ =\sqrt[]{16+6}4 \\ =4\sqrt[]{5} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/lvkdyqr72lepkzz5c6chwsiqkn9x2vfbgh.png)
The radius is,
![\begin{gathered} r=\frac{4\sqrt[]{5}}{2} \\ =2\sqrt[]{5} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/upn7vib2drp0sw4s73bchebej0lgolcjly.png)
The equation for the circle is,
![\begin{gathered} (x-(-12))^2+(y-5)^2=(2\sqrt[]{5})^2 \\ (x+12)^2+(y-5)^2=20 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ey4nemz1hdp8105hhma36nwevbynrfzhcm.png)
Thus, the equation for the circle is (x+12)^2 +(y-5)^2 =20.