SOLUTION
We have been given the height of each lateral triangular face of the roof h as 13.4 ft and the length of the square base of the pyramid as 21.5 feet
We want to know if the area of the square base is the same as the area of each triangular lateral face
Area of the square base is
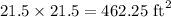
Area of the four triangular lateral face becomes

From our calculations, the area of the square base is 462.25 square-feet,
While the area of the four lateral face triangle of the roof is 576.2 square-feet
Hence the roofer is incorrect