Question

One of the roofers claims that the roof area of each pillar is the same as the area of a square with edges of 21.5 feet.The roofer is correct or incorrect?

Answer 1

We have been given the height of each lateral triangular face of the roof h as 13.4 ft and the length of the square base of the pyramid as 21.5 feet

We want to know if the area of the square base is the same as the area of each triangular lateral face

Area of the square base is

`21.5*21.5=462.25\text{ ft}^2`

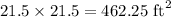
Area of the four triangular lateral face becomes

`\begin{gathered} 4((1)/(2)* b* h) \\ =4*(1)/(2)*21.5*13.4 \\ =2*21.5*13.4 \\ =576.2\text{ ft}^2 \end{gathered}`

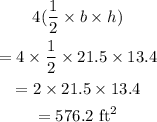
From our calculations, the area of the square base is 462.25 square-feet,

While the area of the four lateral face triangle of the roof is 576.2 square-feet

Hence the roofer is incorrect